Uzumaki: Building Cross-Platform Spiral Visualizations with React, SwiftUI, and Mathematical Precision

Spirals appear everywhere in nature. The nautilus shell grows in a logarithmic spiral, maintaining its shape at every scale. Sunflower seeds arrange themselves in Vogel spirals, optimizing for space using the golden angle. Galaxy arms sweep outward in patterns described by the same mathematics that fascinated Archimedes over two millennia ago.

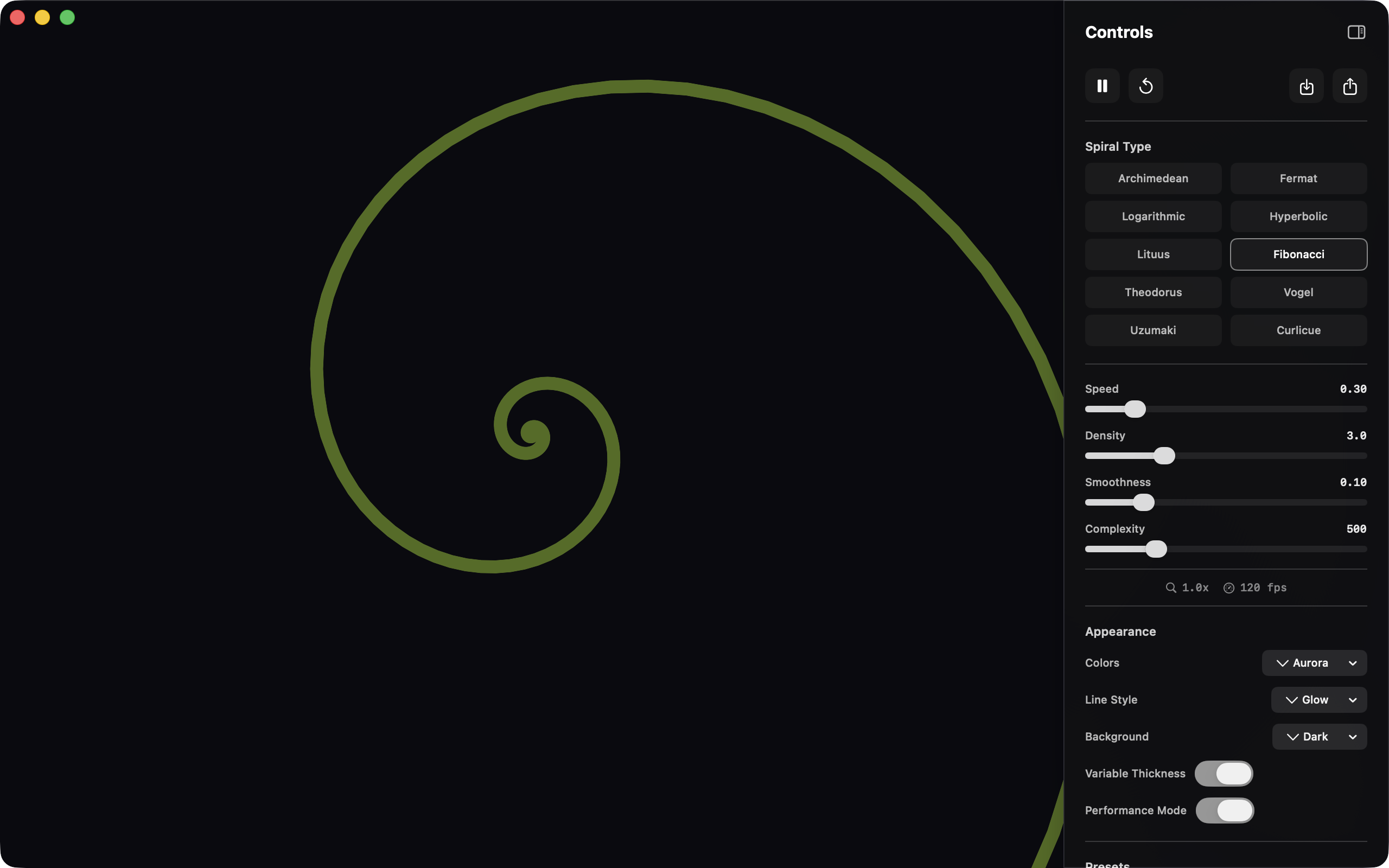
Uzumaki began as an exploration of these mathematical patterns, a way to see the equations that describe natural beauty. It evolved into a cross-platform application spanning six deployment targets: web browser, Progressive Web App, iOS, iPadOS, macOS, and watchOS.

Ten Algorithms, One Canvas

The core challenge was implementing ten distinct spiral algorithms with consistent behavior across platforms. Each spiral type follows a specific mathematical formula, most using polar coordinates where r is the radius and theta is the angle.

Polar Coordinate Spirals

The simpler spirals translate directly from mathematical formulas:

// Archimedean: constant spacing between turns
r = a * theta;

// Fibonacci (Golden): self-similar, found in nature
r = a * Math.pow(PHI, (2 * theta) / Math.PI) * 0.1;

// Logarithmic: equiangular, seen in hurricanes
r = a * Math.exp(0.1 * theta);

// Fermat: parabolic, used in optics
r = a * Math.sqrt(Math.abs(theta)) * 2;

Construction Spirals

Other spirals require iterative construction rather than simple formulas:

// Theodorus: built from right triangles
for (let n = 1; n <= numSteps; n++) {
  angle += Math.atan(1 / Math.sqrt(n));
  x += Math.cos(angle);
  y += Math.sin(angle);
}

// Vogel: phyllotaxis pattern (sunflower seeds)
const GOLDEN_ANGLE = Math.PI * (3 - Math.sqrt(5)); // ~137.5 degrees
for (let n = 0; n < numSteps; n++) {
  const theta = n * GOLDEN_ANGLE + rotation;
  const r = scale * Math.sqrt(n) * 2;
}

The Curlicue fractal produces particularly striking patterns by accumulating angles based on the golden ratio squared.

Web Performance: Workers and TypedArrays

Generating thousands of points per frame while maintaining 60fps required moving computation off the main thread. Web Workers handle spiral generation, but the real performance gain came from TypedArrays.

export function generateSpiralTyped(params: SpiralParams): TypedSpiralPoints {
  const points = createTypedPoints(numSteps); // Float32Array
  const rotation = time * spinRate;

  for (let i = 0; i < numSteps; i++) {
    const theta = i * stepSize + rotation;
    const r = calculateRadius(i * stepSize, params);
    setPoint(points, i, r * Math.cos(theta), r * Math.sin(theta));
  }
  return points;
}

TypedArrays are transferable between the main thread and Web Workers without copying, eliminating serialization overhead. The interleaved [x0, y0, x1, y1, ...] format maps directly to canvas drawing operations.

Swift Parity: SIMD Vectorization

The Swift implementation needed matching performance. Apple’s SIMD framework enables vectorized math operations that process multiple points simultaneously:

func generatePolarSpiral(params: SpiralParams) -> [SIMD2<Float>] {
  var points: [SIMD2<Float>] = []
  let rotation = params.time * params.spinRate
  
  for i in 0..<params.numSteps {
    let theta = Float(i) * params.stepSize + rotation
    let r = calculateRadius(Float(i) * params.stepSize, params)
    points.append(SIMD2(r * cos(theta), r * sin(theta)))
  }
  return points
}

Both implementations follow the same algorithm specification document, ensuring a spiral generated on web looks identical on watchOS.

Maintaining Feature Parity

Cross-platform development often leads to feature drift, where platforms diverge as each adds unique capabilities. Uzumaki maintains parity through:

1. Shared Algorithm Specification: A single markdown document defines exact formulas and edge cases
2. Identical Presets: Both platforms ship with the same ten curated spiral configurations
3. Consistent Color Palettes: Rainbow, Aurora, Neon, Matrix, and six other presets render identically
4. Platform-Appropriate Controls: Touch gestures on mobile, keyboard shortcuts on desktop, Digital Crown on watch

iOS 26 Liquid Glass

Apple’s upcoming iOS 26 introduces the Liquid Glass design language. Uzumaki’s Apple apps include conditional support that activates on iOS 26 while maintaining backward compatibility with current releases. The translucent, depth-aware interface style complements the mathematical visualizations without competing for attention.

watchOS: Spirals on Your Wrist

The watchOS implementation presented unique constraints. The small display demands aggressive simplification, but spirals remain visually compelling even at reduced complexity.

Key adaptations for watchOS:

• Digital Crown: Smooth zoom control with haptic feedback at preset boundaries
• Swipe Navigation: Horizontal swipes cycle through preset configurations
• Complications: Circular, corner, rectangular, and inline complications show static spiral art
• Tap Gestures: Single tap toggles animation, double tap resets zoom

The watch complications transform the utilitarian watch face into dynamic art, displaying a different spiral preset each hour.

Shareable URLs

One feature absent from native apps appears on web: shareable URLs. Every spiral configuration encodes into a URL that recreates the exact state:

export function encodeState(params: SpiralParams): string {
  const state = {
    t: params.type,
    c: params.colorPreset,
    s: params.tightness,
    r: params.spinRate,
    z: params.zoom
  };
  return btoa(JSON.stringify(state));
}

Users can share spiral creations by copying the URL. The recipient sees the identical animation without any configuration.

Lessons Learned

Canvas rendering scales remarkably well. Both HTML Canvas and SwiftUI Canvas handle thousands of animated points at 60fps when computation moves off the render thread.

TypedArrays are underutilized. Most JavaScript developers default to regular arrays. For numerical computation, Float32Array offers significant performance gains and enables zero-copy Worker communication.

Algorithm documentation prevents drift. Without a formal specification, subtle differences accumulate between implementations. The shared algorithm document caught several bugs during development.

Platform idioms matter. Users expect swipe gestures on iOS and keyboard shortcuts on desktop. Forcing identical interaction patterns across platforms feels unnatural.

---

Explore mathematical spirals at uzumaki.app or browse the source code on GitHub. Download for iOS and iPadOS or macOS on the App Store.